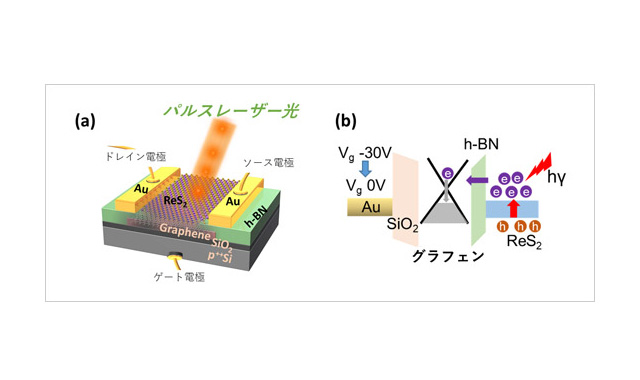
- 2019-4-22
- 制御・IT系, 技術ニュース, 海外ニュース
- Andrew Booker, Tim Browning, ブリストル大学, 学術, 方程式, 立方数
Lucy Reading-Ikkanda/Quanta Magazine
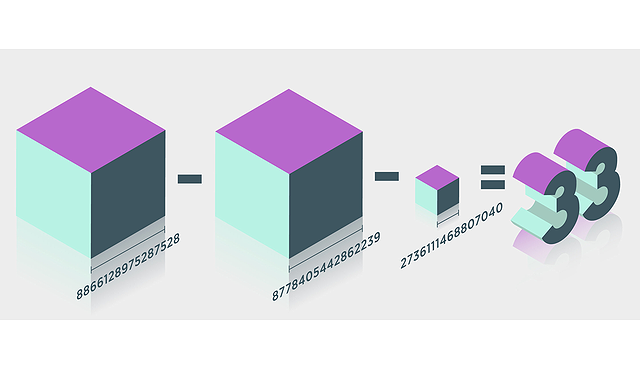
ブリストル大学の数学者Andrew Booker氏が、33を3つの立方数の合計で表すこと、すなわち33=x³+y³+z³という方程式の解を求めることに成功した。16桁(1000兆)という正と負の整数の組み合わせを効率的に探索できるアルゴリズムを開発し、(8,866,128,975,287,528)³+(-8,778,405,442,862,239)³+(-2,736,111,468,807,040)³=33であることを明らかにした。
k=x³+y³+z³の方程式を満たす3組の整数(x,y,z)を求めるという問題は、数学者たちを長年魅了し続けてきた。k=29のように解を容易に導き出せる場合や、9で除したときに4か5が余りとして残る整数、例えばk=32のように解が存在しないことが分かっている場合もあるが、大抵の場合において解は自明ではない。今のところ、解を発見する唯一の方法は、コンピューターを使って総当たりで宝くじを引き続けるだけだ。
世界中の数学者たちは1955年以来、利用可能な最も強力なコンピューターを用い、解を導き出してきたが、いくつかのkについては未だに当たりくじを引けていない。100以下の整数の中で、解のないものを除いて、解が分かっていない2つの整数は、33と42だ。
1955年から、Booker氏が33の解を発見するまで実に64年もの時を要した。ここまで長い時間がかかった理由は、(x,y,z)の正しい組み合わせを求めるために、正負の整数を1016(1京)まで検索することが、Booker氏の新アルゴリズムが誕生するまで不可能だったからだ。オーストリアの数学者であるTim Browning氏は「彼は10年前に比べてより高性能なコンピューターでアルゴリズムを走らせただけでなく、解を導くための本当にもっと効率的な方法を編み出した」と、Booker氏の研究を評する。
Booker氏のアルゴリズムは、kを従来の約20倍の速度で検索することができるという。彼はそのアルゴリズムを大学のスーパーコンピューターで、3週間連続して走らせて解を導いた。Booker氏によると、解が出るのに6カ月くらいかかると思っていたが、予想より早かったという。同氏の次なる目標は、もちろんk=42の解を見つけることだ。