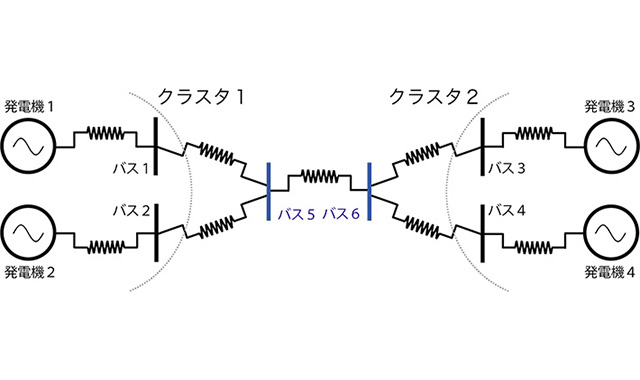
バス(連結点)に関して対称な電力ネットワーク例
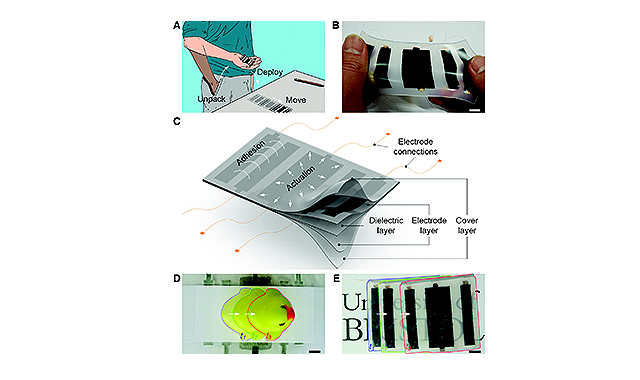
東京工業大学は2018年5月2日、電力ネットワークのモデリングや解析、制御に関する一連の研究成果をグラフ理論により検討し、ネットワーク結合された発電機群の同期を実現するための基本原理を明らかにしたと発表した。ネットワークの対称性が発電機群を同期させることを証明し、発電機群の振る舞いを効率的に解析、制御できる電力ネットワークの集約モデルを構築する手法を開発した。
火力発電所など複数の発電機群の回転子の位相角が揃う「同期現象」は、電力の安定供給のために重要で、ある発電機が同期しなくなると運転が不安定となり、最悪の場合、停電などを引き起こす。今後、発電量が不規則に変動する再生可能エネルギーによる発電の導入が進めば、発電機群の同期の維持はより重要となる。しかし、この同期現象の解析は、従来数値シミュレーションに基づくアプローチが主流で、その原理を理論的に明らかにした研究はなかったという。
送電網でネットワーク結合された発電機の振る舞いは、微分方程式と代数方程式をまとめた微分代数方程式で表現されるが、解析の際には、Kron縮約と呼ばれる簡略化手法によって、微分方程式に変形されて行われるのが一般的だ。しかし、それによって送電網を表す代数方程式が消去されてしまい、送電網のネットワーク構造と発電機群の同期現象の解析には不向きだった。
今回の研究では、グラフ理論という数学理論により、代数方程式に含まれる送電網のネットワーク構造の解析を行った。グラフ理論とは頂点(ノード)の集合と辺(エッジ)の集合で構成されるグラフ(ネットワーク構造)に関する理論だ。解析の結果、送電網の対称性(グラフの頂点の配置位置の入れ換えに関してグラフ構造が不変であること)が発電機群の同期を実現する基本原理であることが明らかになった。
さらに、同期している発電機群とそれらを結合する送電網を同時に集約するという新たな着想を加えた電力ネットワークの集約モデル(冗長な変数を集約して得られる微分代数方程式モデル)を構築した。従来の集約モデルはKron縮約モデルから構築されていたため、現実の電力ネットワークにおいて成り立つ物理法則が反映されていなかった。
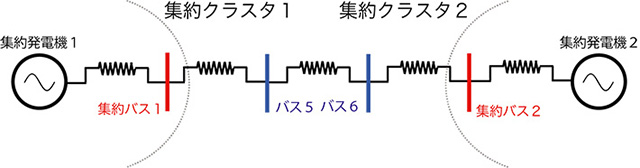
集約された電力ネットワーク
今回の研究成果は今後、電力を安定供給するための解析/制御手法を開発する基盤としての発展が期待される。