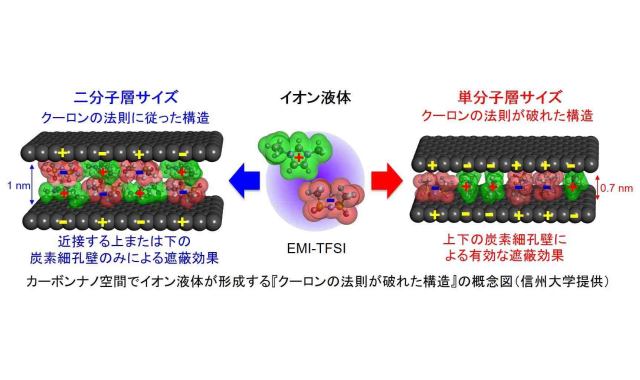
- 2021-6-11
- 化学・素材系, 技術ニュース, 海外ニュース
- Barak Kol, Celestial Mechanics and Dynamical Astronomy, カオス的性質, ニュートン, ヘブライ大学ラカ物理学研究所, ポアンカレ, 三体問題, 位相空間, 天文学, 学術, 物理学

「三体問題」は、空間において重力相互作用する3個の物体の動きを予測する問題。物理学や天文学の問題を理解するための本質的な課題として、ニュートン以来3世紀以上にわたり、世界的な物理学者、天文学者、数学者などの心を捉えてきた。彼らのこの課題に対する試みは科学においていくつか重要な分野を切り開いてきた。しかし、三体問題はいまだ完全には解かれていない。
19世紀後半、数学者ポアンカレは、三体問題にカオス的性質があることを提示した。その後、コンピュータの発展により、シミュレーション手法で三体問題のカオス的性質が詳細に調べられようになる。この手法では、明確で信頼のおける長期予測ができないことが分かった。そして1976年、三体問題の解析に統計論的な手法が導入され議論はさらに発展していく。
今回、ヘブライ大学ラカ物理学研究所Barak Kol教授による三体問題における新しい研究が『Celestial Mechanics and Dynamical Astronomy』誌に2021年4月1日付で公開されている。成果は、この数世紀にわたる未解決問題への統計論的アプローチとなっている。
2019年に、ラカ物理学研究所のStone博士らは、初めて三体問題の統計論的解のための閉じた数学的表現を発表した。しかしながら、この方法は、これまでの統計論的アプローチと同様にある特定の仮定に依存していた。
物理学における統計理論の基礎となるのは、「位相空間」の概念であり、ある事象が起こる確率は、付随する位相体積として考える。ところが、三体問題は無限の系であり、無限の位相体積を持ち、無限の確率という矛盾を示す。この矛盾を解決するために、これまでは「強い相互作用領域」を仮定し、外側の位相体積を無視することで有限としていた。しかし、重力は距離とともに小さくなるが、決して消えることはない。そのため、モデルに任意性を導入する必要があった。
今回、Kol教授の研究では、位相体積そのものより、位相空間からの出力流速に注目した。体積が無限なときでも流速は有限であり、新しいアプローチでは、任意性のある「強い相互作用領域」を導入せずに無限の確率という矛盾を回避できる。
Kol教授は、何百万回ものテストで、理論とシミュレーションの高い一致を示していると強調する。この一致は、三体問題の理解はパラダイムシフトを必要とし、新しいアプローチはよくシステムを説明することを証明しているという。