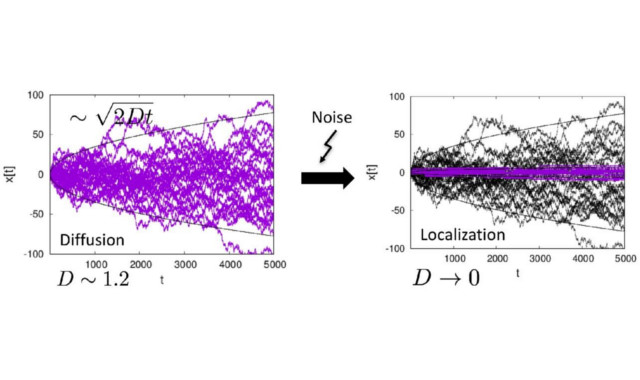
多数の粒子の軌道を表した図。拡散運動に外部から撹乱を加えると、拡散係数Dが0の異常劣拡散運動が生じて大多数の粒子が初期状態付近に長時間滞留する
北海道大学は2019年5月14日、ロンドン大学と共同で、ノイズの伴う開放力学系における非定常な確率カオスと異常拡散を発見し、ランダム力学系理論、連続時間酔歩理論によりその生成メカニズムと普遍性を明らかにしたと発表した。
水中にインクの滴を落とすと、かき混ぜなくてもインクがゆっくりと水全体に広がっていく。この現象は拡散とよばれ、ミクロでは多数のインクの粒子が乱雑な運動の結果散らばり、空間的に徐々に広がっている。この広がりの強さは粒子分布の分散の時間的な増大率で特徴付けられ、この増大率は拡散係数と呼ばれる。この拡散係数が0(または無限大)の極端に遅い(速い)拡散を「異常拡散」という。一般に拡散運動はランダム運動をする粒子集団によってモデル化可能だ。
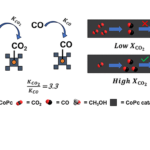
一方、両端の開いたビリヤード系の中にある粒子集団の「カオス散乱」を用いた拡散のモデル化も存在する。開放ビリヤード系に粒子を入射すると、入射の初速度や初期位置が少しずれただけでその散乱軌道は全く異なったものになる。この初期値鋭敏性を伴う散乱運動をカオス散乱という。このようなランダム性の全くない開放ビリヤード系のような力学系での拡散現象は「決定論拡散」と呼ばれる。特に、異なる準定常状態に長時間滞留しつつ、不規則に遷移する非定常ダイナミクスである「間欠性」をもつ開放力学系は異常拡散を示すことがある。
今回研究グループは、拡散現象を示す開放ビリヤード系において、その外壁をゆする、ゆがめる、外部からの撹乱を与えるといったモデルの拡張をしたとき、内部の拡散運動はどう変化するかを、ノイズのある環境下で決定論的運動を記述する「ランダム力学系理論」を用いて解明した。

両端の開いたビリヤード系で生じる拡散現象
最初に研究グループは、安定なダイナミクスを持つ力学系と不安定なダイナミクスを持つ力学系を確率的に混合するランダム力学系モデルを作成。数値実験により、このモデルが非定常な確率カオス(統計的な意味で初期値鋭敏性を有する確率ダイナミクス)と異常劣拡散(遅い拡散)を示すことを確認した。
加えて、ランダム力学系理論による解析で非定常な確率カオス(確率間欠性)の存在が示された。さらに「連続時間酔歩理論」による解析でその異常統計性を特徴づけた。また、モデルを拡張して異なるタイプの力学系とノイズを組み合わせた場合にも同じ結果が得られたことで、今回発見された「ノイズによって誘起される確率間欠性と異常拡散」の普遍性も示した。
この研究により、ランダム力学系の確率間欠性によって生成される異常拡散という普遍的な現象が、流体・気象現象、さらに経済・社会の輸送現象、生物集団の運動などで見出されていくことが期待されるという。また、ランダム力学系理論と連続時間酔歩理論に基づく異常拡散運動の解析により、確率過程論や力学系理論、非線形非平衡系の物理学の深化が見込まれる。さらに、今回のモデル化手法と解析法は、実験的に観察されている様々な拡散現象を分析する有力な方法になることが期待されるという。