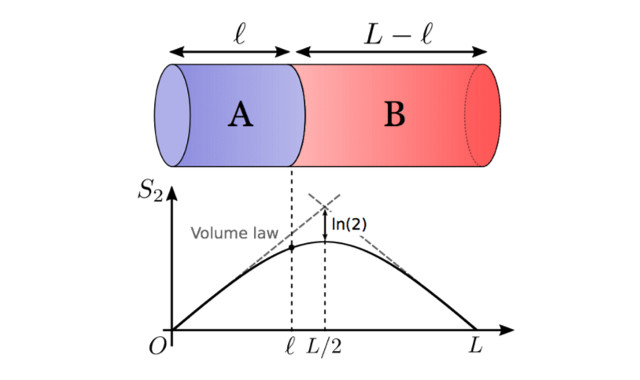
量子もつれの空間分布のグラフ。物質をAとBの2つに分けたとき、AとBの間にどのくらいの量子もつれが生じているかを縦軸に、物質Aの長さを横軸にプロットした図
東京大学は2018年4月24日、同大学の研究グループが、量子純粋状態かつ平衡状態になっている時の、量子もつれの空間分布を完全に決定したと発表した。この空間分布は熱力学エントロピーのみによって決まり、物質の種類や平衡状態の作り方を変えても常に同じ分布であることを実証。この理論は、宇宙に存在するブラックホールから半導体中の電子まで、広範囲に適用可能だという。
ミクロな世界を記述する量子力学と、マクロで普遍的な性質に着目する熱力学との理論的な対応関係は、20世紀初頭の量子力学の黎明期から研究されてきた。その中でも、熱源と完全に切り離された量子純粋状態を用いた熱力学の構築は、実験的観点からも重要視されている。
このミクロとマクロの対応の研究では量子もつれが重要になる。量子もつれとは、空間的に離れた2つの量子状態が互いに影響し合う現象だ。量子もつれによって、量子テレポーテーション、ブラックホールの蒸発現象などの様々な現象が理解できる。
量子純粋状態を用いた熱力学では、量子もつれの量が熱力学的なエントロピーに対応する。熱平衡は熱力学のエントロピーの増大によって起こる。そのため、量子力学の観点では、熱平衡は系全体に量子もつれが広がることで起こる現象と言うことができる。平衡状態の中では大量の量子もつれが複雑に絡み合っているため、どの程度の量の量子もつれが生じているのかを予言できる一般論は、これまで存在していなかった。
同グループは熱平衡状態を表す量子純粋状態における量子もつれの空間分布を研究。量子純粋状態にある系を空間的に2つに分けた時に、その二つの領域間に存在するエンタングルメント・エントロピーという量子もつれの度合いがどのような性質を持つかを調べた。
研究ではまず、熱力学系との厳密な対応が確立されているcanonical thermal pure quantum state(cTPQ)という量子純粋状態に基づき、エンタングルメント・エントロピーの空間分布を表す一般的な関数を導き出した。また、その関数が別の様々な量子純粋状態の量子もつれの空間分布に対しても共通によく当てはまることを確認。これにより、熱力学系と対応する量子純粋状態におけるエンタングルメント・エントロピーが普遍的な性質を持つことを示した。
この研究で見出された普遍的性質を用いることで、冷却原子系やイオントラップ系といった外界から孤立した量子系の実験データから、その量子系の量子もつれを高精度に解析することが可能になるという。