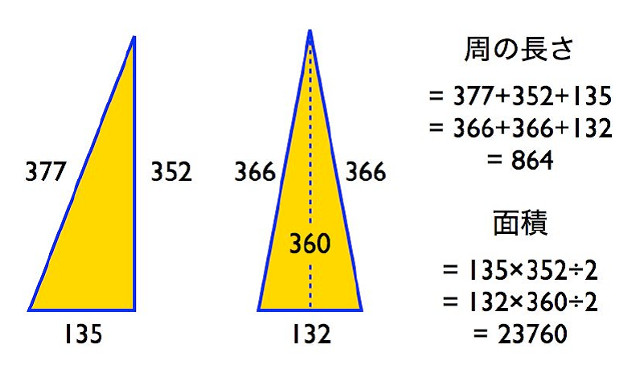
見つかった三角形の組
慶應義塾大学の研究グループは2018年9月12日、「辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には、周の長さも面積も共に等しい組が(相似を除いて)たった1組しかない」という、これまで知られていなかった定理の証明に成功したと発表した。この定理は一見初等的であるが、証明には20世紀末に開発された比較的新しい「数論幾何学」の手法が用いられている。高度に抽象化された現代数学において、このような身近な応用例が得られることは非常に珍しいという。
線の長さや図形の面積は、身の回りにあるものを測量する際に欠かせない基本的な幾何学的対象だ。例えば、辺の長さが3、4、5の直角三角形は教科書でもおなじみの図形であるが、「辺の長さが全て整数となる直角三角形はどのくらいあるか?」という問題は古代ギリシャ時代から研究されてきた。同様に、「辺の長さが全て整数となる直角三角形の組の中には、周の長さも面積も共に等しい組がどのくらいあるか?」という問題なども、研究されていたと推測される。
これらの問題は、全て「種数0の代数曲線上の有理点集合の決定」という問題に言い換えることができる。代数方程式の解集合として定まる図形を代数多様体と呼び、特に1次元の図形は「代数曲線」と呼ばれる。代数曲線の例としては、xy-平面内の直線 y = xや放物線 y = x2、円周 x2+y2 = 1などが挙げられる。また、方程式の複素数解集合から定まる代数曲線は、浮き輪がいくつか連結した図形と同一視できる。この浮き輪の数が種数だ。直線、円周、放物線の種数は0だ。有理点とは、代数多様体上の点のうち、代数方程式の有理数解に対応する点を有理点という。
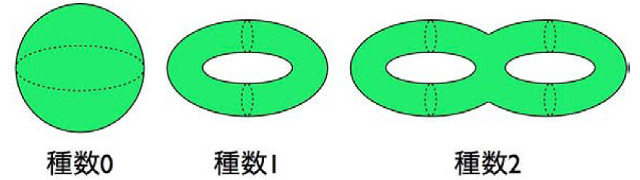
種数0の代数曲線上の有理点集合の決定の問題は「有理一意化」と呼ばれる手法により解けることが、少なくとも座標幾何学が誕生した17世紀には知られていた。しかし、Fermat(フェルマー)方程式 xn+yn = 1のような「種数1以上の代数曲線上の有理点集合の決定」に帰着される問題には、現代でも統一的な解法が知られていない。この難問の解決に動機付けられて、20世紀に現代数学の1分野である数論幾何学が大きく発展した。
研究グループは「辺の長さが全て整数となる直角三角形と二等辺三角形の組の中には、周の長さも面積も共に等しい組が(相似を除いて)たった1組しかない」という定理を証明するため、まず問題となっている三角形の組を種数2の代数曲線でパラメーター付けし、「特殊な種数2の代数曲線上の有理点集合の決定」という別の問題に帰着させた。このような代数曲線上には有理点が有限個しかないことは知られていたが、有理点集合を完全に決定するためにはさらに高度な技術が必要になる。そこで研究グループは、「p進Abel積分論」に基づいた「Chabauty-Coleman法」と呼ばれる解析的な手法を用いて、有理点が10個しかないことを証明した。
得られた10個の有理点のうち、8個は「辺の長さが0または負となる潰れた三角形の組」であったが、残りの2個の三角形は周の長さと面積が共に等しい組であることが分かった。また、研究グループはChabauty-Coleman法適用の前提条件が満たされていることも「2-降下法」というコホモロジーの手法を用いて証明している。
今回解決した問題は古代ギリシャ時代にも考察されていたと考えられているが、証明に用いられたChabauty-Coleman法と2-降下法は共に1980年代以降に開発され、比較的新しい。高度に抽象化された現代数学において、このような身近な応用例が得られることは非常に珍しいという。