算数でのつまずきをなくそう――直線図やボックス図を取り入れた新しい教育手法を考案

• Tweet
• 

© UNIGE

小学校で習う算数には、いくつかのつまずきポイントがある。6～7歳の児童の場合、足し算や引き算の問題を解く際に、無意識に問題が示す状況を頭の中で思い描く傾向がある。しかし、問題が複雑になると、イメージを使って考えることができなくなるか、間違った答えを出してしまう。

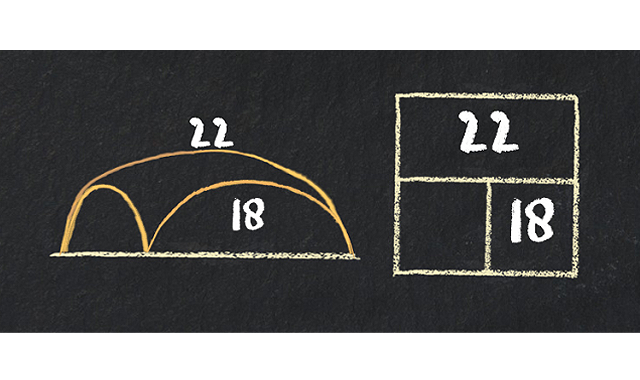
スイスのジュネーブ大学（UNIGE）の研究チームは、算数で抽象的な原則を使用させる「ACE-ArithmEcole」方式を考案した。ACE-ArithmEcoleでは直線図やボックス図を利用して、直感や日常生活から得た知識の代わりに、抽象的な原理を用いて考えるようになるという。

研究チームは、6～7歳の児童（日本での小学1年生に相当）が在籍する10クラスを対象に比較実験を行った。半分の5クラスでは従来どおりの授業を行い、残りの5クラスではACE-ArithmEcoleを実施して抽象的な考え方を好むように働き掛けた。

「生徒に意味の再符号化を実践させるため、直線図やボックス図といったさまざまなツールを与えたのです」とUNIGEのEmmanuel Sander教授は語る。

そして1年後、ACE-ArithmEcole方式の効果を確認するため、足し算や引き算を使う文章題のテストを実施した。問題は「結合」「比較」「変化」の3タイプで、状況をイメージしやすく日常生活から得た知識で解けるものと、イメージしにくく算術的原理を用いる必要があるものの両方が出題された。

テストの結果は、興味深いものとなった。ACE-ArithmEcole方式で教わった生徒では、イメージしやすい簡単な問題の正答率が63.4％、イメージしにくい難しい問題の正答率は50.5％だった。ところが、従来どおりの授業を受けた生徒では、簡単な問題の正答率は42.2％、難しい問題では29.8％と、両者には差が見られた。

このような差は、ACE-ArithmEcole方式で教わったことで、生徒がイメージを思い浮かべて考えるのではなく、算術的原理の方を頻繁に利用するようになったからだと説明できるかもしれない。ACE-ArithmEcole方式は抽象的な考え方を促進し、頭の中でシミュレーションするやり方から脱却するための基礎を養うという。

「この授業方法を高学年の授業へ広げたいし、掛け算や割り算にも取り入れたい」と、Katarina Gvozdic研究助手は語る。この方式は、直感的な思考が学習の妨げとなり得る科学や文法といった他の科目にも応用できる可能性があるという。

関連リンク

A new method for boosting the learning of mathematics
Learning to be an opportunistic word problem solver: going beyond informal solving strategies