ディープラーニングAIがシュレーディンガー方程式を解く

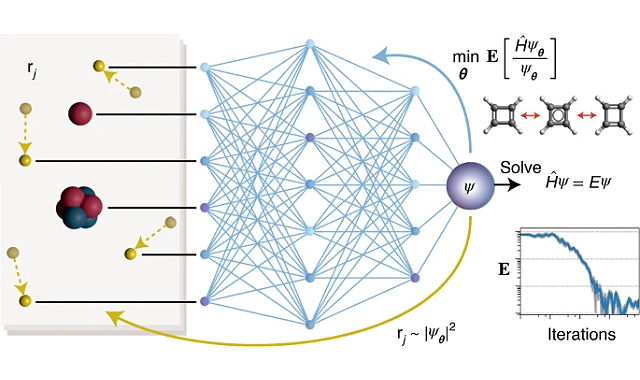
独ベルリン自由大学は、2020年12月18日、量子化学におけるシュレーディンガー方程式の基底状態を計算するために使う人工知能（AI）手法を開発したと発表した。研究成果は『Nature Chemistry』に2020年9月23日付で掲載されている。

量子化学では、時間がかかり資源を消費する研究室での実験を避け、空間内の原子配置にのみ基づいて分子の化学的および物理的性質を予測することを目標として、研究が進められている。原理的には、これはシュレーディンガー方程式を解くことで実現可能だという。しかし、シュレーディンガー方程式の解法の研究では、分子内の電子の振る舞いを完全に規定する波動関数がメインに扱われるが、波動関数は高次元の実体であるため、個々の電子がどのように相互に影響しあうかを全てとらえることは非常に難しいという。

そこで、実際には波動関数を完全に表すことを諦め、代わりに与えられた分子のエネルギーのみを決定する手法が取られる。しかし、この手法では近似が必要となり、予測精度が制限されてしまう。他にも、膨大な数のシンプルな数学的構成要素を用いて波動関数を表現する方法もあるが、非常に複雑で、応用できる原子も少ないという。現在のところ、精度と計算効率との間のトレードオフ回避という点では、非常に計算コスト効率が高い密度汎関数理論がメジャーな手法となっているが、今回提案された深層学習（ディープラーニング）型波動関数解法は、密度汎関数理論の手法と同等かそれ以上の成果が期待できるようだ。この深層学習型解法では、ハートリー・フォック法をベースに、変分量子モンテカルロ法を用いて学習する。

今回、研究者らが開発した高精度と高い計算効率を同時に達成できるディープラーニング手法では、最大30個の電子を持つ分子の電子シュレーディンガー方程式のほぼ正確な解を見つけられるという。研究では、比較的シンプルな数学的要素から波動関数を構成するという標準的なアプローチではなく、電子がどのように原子核の周りに配置されているかという複雑なパターンを学習できる人工ニューラルネットワークを設計したという。電子波動関数の特徴の1つに、2つの電子が交換されると波動関数は符号を反転させなければならないという反対称性があるが、研究者らはこの特性をニューラルネットワーク構造に組み込む必要があった。この特徴は「パウリ（Pauli）の排他原理」と呼ばれているため、研究者らは今回開発した手法を「PauliNet」と名付けている。

開発されたPauliNetの革新的な点は、ディープラーニングにデータ観察だけでデータを解明させるのではなく、電子波動関数が持つ他の物理的性質をディープニューラルネットワークに統合した点にある。研究チームを率いたFrank Noé教授は、基本的な物理学をAIに組み込むことはこの分野で意味のある予測を行うために不可欠だとしている。

PauliNetはまだ開発段階であり、産業への応用には課題が多数残っているようだが、PauliNetによる新しいアプローチは分子／材料科学の発展に貢献することが期待される。

ディープラーニングAIがシュレーディンガー方程式を解く