- 2024-10-17
- 制御・IT系, 機械系, 研究・技術紹介, 電気・電子系
- 2次元直交座標系, GPS(Global Positioning System:全地球測位システム), サモスの賢人, ピタゴラス, ピタゴラスの定理(三平方の定理), ピタゴラス数, レーザー距離計, 図形問題, 数学, 直角三角形, 直角二等辺三角形, 自然数, 鉤股弦の法(こうこげんのほう)」
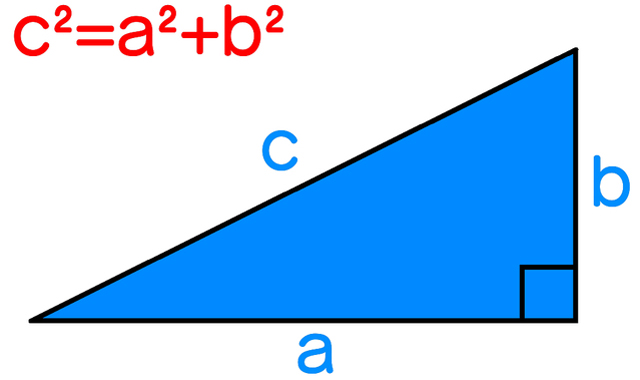
ピタゴラスの定理(三平方の定理)は、中学3年生で習う数学の公式です。図形問題を解くのに欠かせない公式ですが、この公式は数学の問題を解くためだけのものではありません。
実はピタゴラスの定理は、さまざまな製品やテクノロジーに活用されています。このことを知っている人は意外と少ないのではないでしょうか。
この記事では、ピタゴラスの定理を簡単に解説し、身近なものに使われている事例なども紹介します。どうぞご覧ください。
ピタゴラスの定理(三平方の定理)とは
ピタゴラスの定理(三平方の定理)とは、「直角三角形の2辺a、b上の正方形の面積の和は、斜辺c上の正方形の面積に等しくなる」という定理です。中国では「鉤股弦の法(こうこげんのほう)」とも呼ばれています。
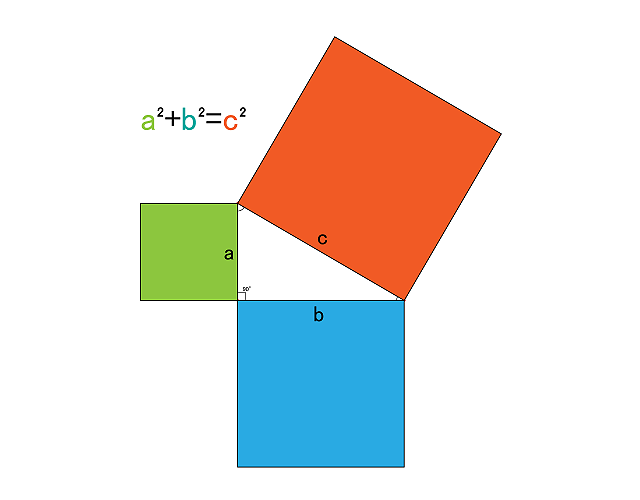
数式では「a2+b2=c2」と表され、直角三角形の3辺のうち2辺の長さが分かれば、残り1辺の長さが計算可能です。なお、ピタゴラスの定理の証明方法は、数百通りあるとされています。
また、ピタゴラスの定理を満たす自然数「a、b、c」の組み合わせは「ピタゴラス数」と呼ばれ、「3、4、5」「5、12、13」「7、24、25」などがあります。
定理名の由来になっている「ピタゴラス」は、古代ギリシャの数学者および哲学者の名です。ピタゴラスはエーゲ海東部に位置するギリシャのサモス島に生まれ、「サモスの賢人」と称されました。
ピタゴラスの定理(三平方の定理)を応用した計算問題
ピタゴラスの定理(三平方の定理)を応用すれば、2次元直交座標系における2点間の距離を求めることができます。例えば、点A(1, 2)、点B(4, 6)間の距離cを求める計算式は、以下の通りです。
c2 =(4−1)2+(6−2)2
c2 = 32+42
c2 = 9+16
c2 = 25
c > 0より
c = 5
また、直角二等辺三角形の長辺の長さを√2とすると、短辺の長さaは以下のように求められます。
a2+a2 =(√2)2
2 a2 = 2
a2= 1
a > 0より
a = 1
ピタゴラスの定理(三平方の定理)が使われている身近な事例

ピタゴラスの定理(三平方の定理)が身近なものに使われている事例として、以下の2点を解説します。
• レーザー距離計
• GPS
それぞれ見ていきましょう。
レーザー距離計
距離を測るツールといえばメジャー(巻尺)ですが、近年はレーザー距離計が使われることも多くなりました。建築や土木などの工事のほか、ゴルフなどでも利用されています。
レーザー距離計はレーザーを対象物に照射し、反射して戻ってくるまでの時間を測定して距離を計算します。対象となるポイントを2点にし、レーザー距離計をもう1つの頂点とする直角三角形を作れば、2辺の長さが分かるため、ピタゴラスの定理でポイント間の距離も測定できます。
例えば、離れた場所にある建物の高さを測りたい場合、地面に置いたレーザー距離計から建物までの水平距離が30m、建物頂点までの距離が50mだったら、建物の高さは40mと計算されます。
GPS
カーナビやスマートフォンなどで利用されるGPS(Global Positioning System:全地球測位システム)にも、ピタゴラスの定理が使われています。
GPSで位置情報を特定するために使用される人工衛星は、高度約2万kmの軌道を周回しています。人工衛星から地球に向かって真っすぐに線を降ろしたとして、その線が直角三角形の「高さ」になります。
一方、人工衛星は電波を発しており、カーナビやスマートフォンなどの端末が電波を受け取るまでの時間によって、人工衛星から端末までの距離を割り出すことが可能です。その距離が、直角三角形の「斜辺」の長さになります。
こうして直角三角形の高さと斜辺の長さが分かるので、ピタゴラスの定理で「底辺」の長さを求められます。しかし、人工衛星が1つだけだと、位置情報としては「底辺の長さを半径とする円周上のどこかにいる」ことまでしか分かりません。そのため、GPSは人工衛星を3つ使い、3つの円を重ねて位置を特定します。
厳密には、時間を補正する人工衛星がさらに1つ加わり、合計4つの人工衛星が使われます。
まとめ
ピタゴラスの定理(三平方の定理)を解説しました。「a2+b2 = c2」というシンプルな数式により、直角三角形の2辺の長さが分かれば、残り1辺の長さを求められます。数学の問題を解く公式としてだけでなく、レーザー距離計やGPSなど、身近な製品やテクノロジーにも使われています。
関連情報
2000年間「不可能」だったピタゴラスの定理の解法を高校生が発見
ライタープロフィール

fabcross for エンジニア 編集部
現役エンジニアやエンジニアを目指す学生の皆さんに向けて、日々の業務やキャリア形成に役立つ情報をお届けします。