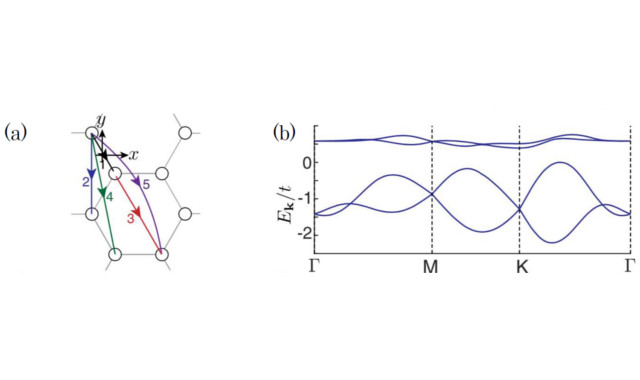
(a)「脆弱なトポロジカル絶縁体」の模型の概略図 (b)「脆弱なトポロジカル絶縁体」のバンド構造
東京大学は2018年9月12日、米ハーバード大学や米マサチューセッツ工科大学と共同で、トポロジカル絶縁体と普通の絶縁体の中間の新しい絶縁体が存在することを理論的に解明したと発表した。物質のトポロジーを利用した新デバイスの発明や、スピントロニクス技術の発展、量子コンピュータの開発などに将来的に結びつく成果だという。
従来、身の回りの物質は伝導性や磁性といった性質に着目することで分類していた。しかし今世紀に入り、数学の分野の1つである「トポロジー」の違いによっても物質の性質が大きく変わることが明らかになり、物質のトポロジカルな性質は世界中で盛んに研究されるようになった。
トポロジーは、滑らかな変形に対して不変に保たれる性質を対象とする。例えば、ドーナツとコーヒーカップはどちらも穴が1つ(ドーナツでは中心の穴、コーヒーカップではとっての部分の穴)という点でトポロジカルに同じであると言われる。
「トポロジカル絶縁体」は、物質内部は絶縁体なのに物質表面は金属になるという性質をもっている。この性質はスピントロニクスの分野に応用されており、低消費電力もしくは高速な次世代のデバイスや量子コンピュータなどの開発につながると期待されている。
近年の物性物理学においては、このトポロジカル絶縁体の候補となる物質を探す応用的研究の他に、「互いに異なるトポロジカル絶縁体はどれだけの種類があるのか」という分類の完成を目指す研究に、世界中の理論物理学者が励んでいる。
そうした中、東京大学の渡邉悠樹講師らの研究グループは「脆弱なトポロジカル絶縁体」という、これまで知られていなかったタイプのトポロジカル絶縁体を発見した。
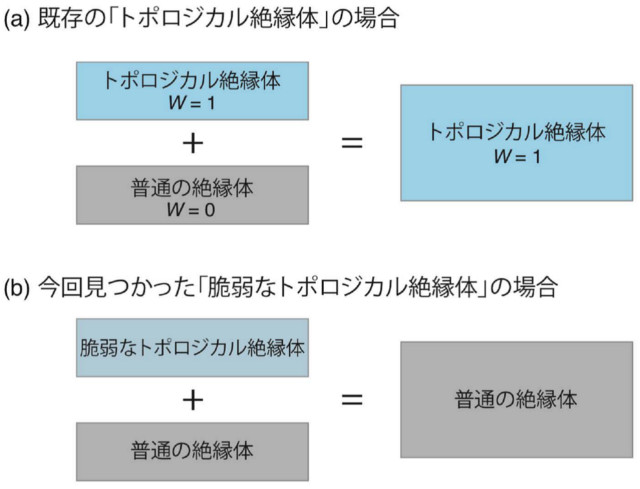
脆弱なトポロジカル絶縁体は、それ自体はトポロジカル絶縁体のように振る舞う。しかし、普通の絶縁体と重ねるだけでトポロジカルな性質を失ってしまうという点が、従来のトポロジカル絶縁体と異なる。通常のトポロジカル絶縁体は「チャーン数」や「Z2トポロジカル数」のような「巻きつき数 W(前述の”ドーナツとコーヒーカップの穴の数”のような、トポロジーを区別する整数の総称)」によって守られているため、普通の絶縁体と重ねてもトポロジカルな性質を失うことは無い。この研究で見つかった例は、トポロジカル絶縁体にはこれまで考えられてきた以上に豊富な種類があることを意味している。
昨年、米プリンストン大学の研究グループが英科学誌ネイチャーに「トポロジカル量子化学(Topological Quantum Chemistry)」という理論を発表し、注目が集まった。脆弱なトポロジカル絶縁体は、この理論の主要な定理に対する反例になっており、今回の研究は基礎理論の進展において重要な意義を持っている。
他にも、今回発見された絶縁体は、超伝導を含む様々な物性を示すことで話題となった「ずらして重ねられた二層グラフェン」の性質にも深く関わっていることが指摘されており、今後のさらなる研究が期待される。













